Reciprocals:
Quotients:
The Pythagorean Identity:
Variations:
All of these equations can be used to simplify an equation or to make sure there is only one trigonometric expression, that way they're so much easier to work with!
And now for some examples!
If cos(x) is .25, then sec(x) is 4.


If cos(x) is 1/5 and sin(x) is 2/5, then cot(x) is 1/2.


Verifying Trig Equations
And now it's time to learn how to verify trig identities! - a.k.a. TRIG PROOFS! (insert ominous music here)
To do this you are given two things that are already equal to each other but are still forced to prove that they are equal through the use of tiny baby steps. The end goal of any trig identity verification is to make the left side of the equation and the right side of the equation look the same.
HOWEVER, this must be done with extreme caution, for ONLY ONE SIDE OF THE EQUATION CAN BE CHANGED. If you ever even think of messing around with the other side of the equation, or even going so far as to CROSS-MULTIPLY, you will be promptly cast into the fearsome pit of trigonometric DOOM!!!!
In order to become a trig proof master, one must follow THE RULES (Actually, they're more like guidelines):
1. Don't lose track of what you are trying to prove. Randomly swapping in trig expressions for other trig expressions doesn't usually work. A better plan would be to look at what the end result should be before diving in. Verifying trig identities is not guess and check. (For an example of guess and check, see 'finding the roots of a polynomial.')
2. Work on making the more complicated side less complicated (or rewrite everything in terms of sine and cosine). Making something more complicated than it already is is generally a waste of time.
3. Work from minor functions (csc, sec, cot, tan) to major functions (sin and cos). This makes sense when you realize that sin and cos are a lot less complicated. (See rule #2)
4. Use the common denominator. When you find a common denominator, you can put two fractions together to form one fraction. And, believe it or not, one fraction is in fact less complicated than two fractions (See rule #2). I know, it's weird, but 1 really is less than 2.
5. Use conjugates. Remember how, in the first section of this post, sin θ was equal to 1 / csc θ? Guess what? It still is! And guess what else? In general, sin θ is a lot less complicated than 1 / csc θ. (Rule #2) Is this starting to sound familiar?
6. Use
 Did you notice that the left hand side is one fraction and the right hand side is two? And did you notice that they all have a common denominator? Does anyone remember rule #4?
Did you notice that the left hand side is one fraction and the right hand side is two? And did you notice that they all have a common denominator? Does anyone remember rule #4?7. Use the Force... just checking to see if anyone was paying any attention.
8. Try not to take the square roots of things or raise them to powers. Remember how we're only supposed to change one side of the equation? If you suddenly make one side exponentially bigger or smaller, what are you supposed to do with the other side to make them match up?
9. Remember:

Last time I checked, trying to put two fractions together by finding a common numerator was not considered to be a very good idea. People who do this are getting way too overexcited about rule #4.
10. A trig proof is like an Oreo cookie. There is always more than one way to verify a trig identity. If your first attempt fails miserably, don't be afraid to go back and try something new!
11. AGAIN, DO NOT CROSS-MULTIPLY! DO NOT ASSUME THE LEFT HAND SIDE EQUALS THE RIGHT HAND SIDE! DO NOT MOVE STUFF FROM THE LEFT SIDE TO THE RIGHT SIDE! DO NOT MOVE STUFF FROM THE RIGHT SIDE TO THE LEFT SIDE! DO NOT PASS GO! DO NOT COLLECT $200! JUST LEAVE THE OTHER SIDE ALONE!
Now let's try a sample identity:

Reminder: Sometimes it is ACCEPTABLE to alter both sides in order to verify a trig proof! However, this should only be done if it SAVES MUCH TIME. Never add or remove anything from either side, or you will suffer chastisment of GREAT VEHEMENCE.
Equation Solving
Equations get MUCH harder once you actually have to figure out what theta or x is.
For example:
3. REMEMBER!!! This is only the reference angle and sin(x) & cos(x) are positive in two quadrants when the period is "0" is less than "x" is less than "360". Keep in mind that tan(x) only has a period of "0" is less than "x" is less than "180".
- sin(x) pos. in Quadrants I,II
- cos(x) pos. in Quadrants I, IV
- tan(x) pos. in Quadrants I, III
Notes:
- If you come across something like sin(2x) then "0" is less than "2x" is less than "360", so "0" is less than "x" is less than "180".
- Sometimes the question will ask for a general solution. This is in the form of {ref. angle + n ● period} where 'n' is an integer.
- Trickier problems involve factoring and replacing some trigonometric expressions with others so only one ends up in the equation
- Radians are also commonly used instead of degrees. Just know that pi = 180 degrees
Equation Solving on T.I.
To solve a trig identity on a TI:
- Equip your TI Graphing calculator.
- Hit mode and set to radians.
- Input the function into Y=.
- Use zoom fit to get appropriate window, or set it manually.
- Hit [Calc], then select "zero", select a point with a positive y value, then a point with a negative y value, then hit enter to find the roots of the function for one period. Avoid ERROR: BAD GUESS.
**Round your answers to the nearest ten thousandth.
**Don't think you're not supposed to write down the viewing window you used.
Sum and Difference Formulas
**With ( A - B ) just reverse the addition/subtraction signs.
Double Formulas
Practice Questions
1) Verify:

2) Verify:

3) Solve for 1 period:

4) Solve for all solutions/general solution (nЄZ):

5) Determine if Schrodinger's cat is alive or dead

6: Derive sin(3x).
7: Verify
8: Solve for 1 period:
10: Solve for x using your TI graphing calcy, 0<= x <= 2pi:

11: If sin(x) = 4/5, sec(x) = ?
12: Verify:
2)
3)
4)
5) Kitteh was dead before he was even placed in box!
6)
7:
8:
9:
10: x = {.793, 1.385, 4.530, 5.634}

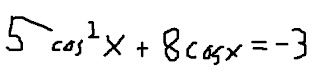
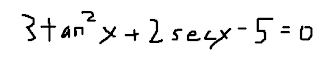
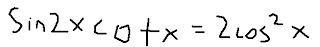

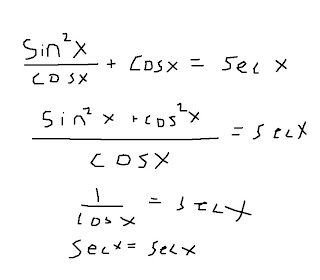
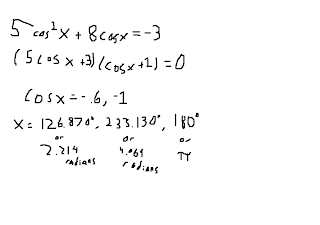

20 comments:
what is up with all of those crappy MS paint pictures
it looks like some 11th grader with ADD made those
also the random capitalization
srsly what
This is clearly the most amazing blog post I have ever seen! Whoever wrote this must be super-amazing!
-P.S. Scott Rocks!
Are you kidding me Matt is way cooler
also that Meroim guy is awesome
No way! Those Matt and Meroim guys both stink!
Your smooth endoplasmic reticulum stinks!
This post is 1% inspiration and 99% perspiration! Also, Scott is way cooler than Matt.
My latest experiments have prooven via the scientific method that
MATT > SCOTT
In response to Mr. Farady's stupid comment, "NO, -2"
Mr. Faraday, you stink at spelling.
Note for next year: only allow comments from registered users.
Neither can you, Mrs. Williams!
so ya matt is better
Can anyone else hear Matt in their head saying "I'm anonymous!"
You are right you are way cooler than me
I can't seem to get 0< x<360 to show up properly. It comes out all weird no matter how I try and type it. Any ideas?
I'd just like to say that Meroim, both Anonymouses, Albert Einstein, Michael Faraday, Mrs. Williams, and Mrs. Weicker are all wrong. It's pretty clear who really is the coolest member of the group.
Never mind, figured it out.
Never mind again, still didn't work.
Jon the inequalities signs signify html tags - I think that is causing your problem. If you only have to type this a few times, I'd just make a formatted latex equation and import the picture. Otherwise...try putting quotes around it? Not sure, maybe someone else will know.
haha, this post was quite helpful, while also enjoyable to read, nice job guys.
Post a Comment